Vous l’aurez compris, le calcul mental ne fait pas exception à la règle. Pour progresser, pas de secret : il faut s’entraîner. À force d’être confronté à plusieurs types d’opérations, le cerveau repère des schémas, mémorise certains résultats, adopte la méthode de calcul appropriée… Il acquiert des automatismes grâce à la répétition quotidienne. Bonne nouvelle : il existe un tas d’outils ludiques et gratuits pour se perfectionner, comme Matheros, Mathador… ou PowerZ et son fameux couloir aux mille portes !
TOP 7 DES ASTUCES DE CALCUL MENTAL : PREMIER EN MATHS !

Qui a déjà vu la méthode Abacus a l’œuvre sait combien elle impressionne. En quelques mouvements de doigts, les enfants qui l’apprennent sont capables de réaliser des opérations complexes en moins de temps qu’il n’en faudrait pour taper sur une calculatrice. Le secret ? Un boulier chinois imaginaire qui permet de noter les retenues et les résultats intermédiaires sans surcharger le cerveau ! En effet, le calcul mental n’est pas une histoire de génie, mais bien d’entraînement. Aujourd’hui, je vous dévoile sept astuces pour progresser et lever la main de la calculette.

Le couloir aux 1000 portes, PowerZ
1. C’est en calculant qu’on devient calculette…
2. Connaître ses tables sur le bout des doigts
Lorsque l’on calcule, plusieurs zones de notre cerveau s’activent, et parmi elles, le lobe temporal médian, généralement impliqué dans la mémoire de long terme. En effet, lorsque vous êtes confronté à une opération complexe, votre cerveau ne repart pas de zéro, mais va puiser dans votre mémoire des brides de solution et les associer pour parvenir au résultat final.
Démonstration par la lecture ! Lorsque vous lisez, vous ne décomposez pas syllabe par syllabe comme si vous redécouvriez chaque mot. De la même manière, vous ne recalculez pas combien font 6x10 et 6x3 chaque fois que vous souhaitez multiplier 13 et 6 ! Les tables sont des résultats mémorisés, immédiatement disponibles. Dans l’enseignement, on les appelle les “faits numériques”. On peut retenir les tables d’addition et de multiplication, ainsi que les compléments de 10 (1 et 9, 2 et 8, 3 et 7…).
3. Apprendre à jongler avec les chiffres : décomposer les calculs
La notion a déjà été introduite implicitement dans l’astuce précédente, mais elle mérite un paragraphe complet, tant elle nous facilite la tâche. J’appelle… la décomposition des calculs ! Pour additionner 93 et 15 sans s’emmêler les pinceaux, on additionne les unités d’un côté et les dizaines de l’autre : 9+1=10 et 3+5=8, donc 93+15=108 !
Ça marche aussi avec les multiplications ! Pour reprendre l’exemple précédent, 13x6 vaut 10x6+3x6=60+18. En fait, on utilise les identités remarquables. En décomposant suffisamment, on en revient systématiquement aux tables apprises par cœur, ces fameux faits numériques.
Pour développer cette souplesse cérébrale qui n’a rien d’inné, les enfants commencent par décomposer les calculs à l’écrit dès le CP, avant de devenir capables de le faire de tête, bien des années plus tard.
4. Passer à la dizaine !
Petit zoom sur une technique de décomposition bien utile : lorsqu’un nombre finit par 8,9,1 ou 2, pensez à passer à la dizaine supérieure ou inférieure. Il est plus facile de résoudre 200+12-1 que 199+12 ! Avec l’entraînement, vous apprendrez à manier les chiffres avec toujours plus de souplesse et de rapidité, en adoptant les techniques qui vous conviennent le mieux. 218+485 ? Facile ! C’est 220+480+3, soit 703. ;)
5. La multiplication par 11
Pour certaines tables, il existe des techniques aussi étonnantes qu’efficaces pour calculer aussi vite que l’éclair sans s’encombrer l’esprit. Voici deux petites astuces pour multiplier un nombre par 11 :
- Multiplier un chiffre entre 0 et 9 par 11 : le chiffre des dizaines et des unités est celui que 11 multiplie. Par exemple, 6x11=66.
- Multiplier un nombre à deux chiffres par 11 : on écrit le nombre et on insère la somme des deux chiffres au milieu, au niveau des dizaines. Ainsi, 45x11=495. Attention, si la somme est supérieure ou égale à 10, on ajoute 1 aux centaines (la retenue).
6. Apprendre à repérer ses erreurs
Lorsque l’on calcule vite, et plus encore de tête, on risque de se tromper. En cas de doute, plutôt que de refaire le calcul entièrement, on peut commencer par intégrer quelques réflexes pour repérer facilement ses erreurs.
Le premier consiste à essayer d’approximer le résultat. Pour cela, on peut supprimer les décimales ou arrondir les nombres à la dizaine. Par exemple, 19x21 est à peu près égal à 20x20. Ou 6,89+10,11 vaut plus ou moins 7+10. D’ailleurs, tant dans le contexte scolaire que scientifique, les approximations sont admises si elles sont présentées rigoureusement.
Ensuite, les règles de divisibilité et autres astuces peuvent vous permettre de repérer certaines fautes. Mais attention, ce n’est pas parce que vous cochez toutes les cases que le compte est bon !
- Le résultat d’une multiplication par 10 finit par 0.
- Le résultat d’une multiplication par 5 finit par 0 ou 5.
- La somme des chiffres du résultat d’une multiplication par 3 est multiple de 3.
- Le résultat d’une multiplication par 2 est pair.
- La somme de deux nombres impairs est paire.
- La somme d’un nombre pair et d’un nombre impair est impaire.
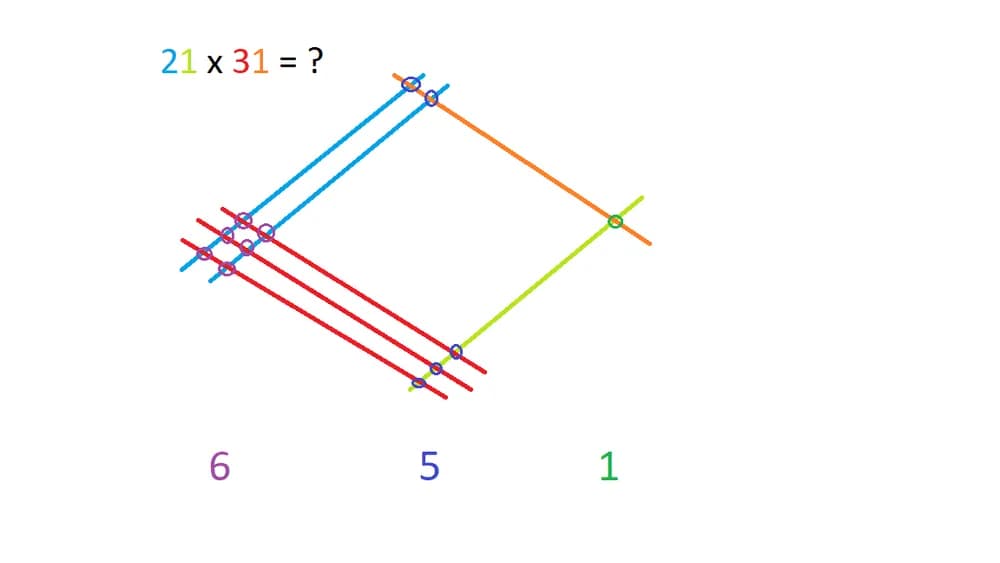
Multiplications : méthode visuelle japonaise
7. La botte secrète japonaise !
Nous arrivons déjà à la dernière méthode, ma préférée. Il s’agit d’une technique japonaise très visuelle pour multiplier deux nombres entre eux sans avoir besoin de poser de calcul. Une illustration valant mieux un long discours, je vous invite à observer l’exemple ci-dessous. Les diagonales ascendantes représentent les dizaines et les unités du premier nombre, tandis que les diagonales descendantes, à lire de bas en haut, correspondent au second nombre. Il suffit de compter les intersections entre les lignes pour obtenir le résultat. Magique !
Chez PowerZ, nous sommes convaincus que l’apprentissage peut et doit passer par le plaisir. Quand on n’aime pas, on n’apprend pas ; et quand on ne sait pas, on n’aime pas. La clé pour progresser, c’est de s’entraîner régulièrement, avec de bons outils… et surtout de s’amuser !